Položili jste si někdy otázku, co se více mění: je to váš podnik a jeho technologické vybavení, nebo se více mění samotné prostředí, ve kterém podniky působí? Aniž bych chtěl podcenit, váš úspěch uvnitř podniku, mám zato, že změna prostředí je větší. Nebo alespoň významnější, chcete-li. Pokud jde o velikost ve smyslu pozornosti, kterou změnám věnujeme, totiž logicky vítězí to, co je u nás, nad událostmi v našem okolí.
V takovém případě může být ovšem snadno zaděláno na problém: okolí se významně mění, zatímco my zůstáváme v zajetí "velkých" změn na vlastním dvorku. Příklad nákladových matic to ostatně demonstruje velmi dobře. Maticová řešení ve vnitropodnikovém zúčtování nákladů byla známa již před osmdesáti lety. Soustavou rovnic a tedy maticí se řešil problém nastavení vnitropodnikové ceny při zacyklení výkonů mezi středisky navzájem, tedy například za situace, kdy údržba poskytuje své výkony dopravě, ale zpětně od ní čerpá některé dopravní služby. Řekněte však pravdu, koho by dnes napadlo něco podobného využít ?
Ano, existovalo hned několik důvodů odvrhnout nepohodlnou matematickou metodu, neboť:
1. přeúčtovávat výkony mezi středisky je nepřesné. Výkony vznikají prostřednictvím procesů, na nichž střediska jako odpovědnostní centra zpravidla spolupracují, servisní úkony pro dopravu tedy neposkytuje středisko údržby, ale vznikají jako výsledek procesu údržby, na němž se podílí mnoho podnikových zdrojů, z nichž na útvar údržby přísluší zřejmě většina, ale rozhodně ne všechny (probíhá údržba aut v dílnách údržbářů? Pokud se udržují vozidla přímo v garážích, je to příklad spotřeby zdrojů (budov) útvaru dopravy. Pokud část banálních úkonů údržby provádějí sami řidiči, jde opět o výkon údržby, personálně zajišťovaný ze zdrojů jiného útvaru atd.). Nákladové ceny, odpovídající nákladům spotřebovaných zdrojů, tedy musí být stanoveny na procesy a uplatňovány přeúčtovávány mezi procesy;
2. výpočet matice bez adekvátní IT podpory je velmi pracný.
Ve skutečnosti však již ani jeden z výše uvedených důvodů neplatí: předně, máme poměrně jasnou představu o tom, jak fungují firemní procesy (často jako vedlejší efekt zavedení systému řízení jakostí). A dále, nikoli nepodstatně se změnily možnosti informačních technologií. Výpočet matice proběhne využitím jediné excelovské funkce a není o nic víc pracný, než například operace typu součtů a průměrů, které běžně využíváme.
Vyzkoušejte si nejprve malý příklad: Podnik je složen ze dvou zcela samostatných divizí, poskytujících si navzájem své (finální) služby. Řídíte například softwarovou firmu, kde ve dvou zcela samostatných budovách s úplným zázemím jsou umístěny programátorská a analytická divize. Každá z divizí si zabezpečuje i potřebnou administrativu vlastními silami.
Jde tedy o dva na sobě zcela nezávislé procesy, s jedinou výjimkou. Analytici spotřebují při svých výkonech ročně 500 hodin služeb programátorů z jejich celkové kapacity 10 tisíc hodin a naopak, programátoři spotřebují z celkové roční kapacity 15 tisíchodin analytiků jednu třetinu, tedy pět tisíc hodin. Roční provozní náklady činí u programátorů 12 milionů korun a u analytiků 18 milionů korun. Jaké jsou náklady na jednu hodinu práce v obou divizích?
Řešení, které by zanedbalo vzájemnou provázanost, určí hodinové sazby obou divizí stejně, podílovou metodou:
celkové náklady / celkové výkony = 12 mio Kč/10 tis. hodin = 18 mio Kč / 15 tis. hodin = 1200 Kč na jednu hodinu,
případně:
celkové náklady/výkony pro zákazníky:
= 12 000 000 / 9 500 = 1263,158 Kč/hod.
pro programátory, resp. pro analytiky:
= 18 000 000 / 10 000 = 1800,000 Kč/hod.
Řešení se vzájemným proúčtováním výkonů bude pracovat se dvěma neznámými hodinovými sazbami xp, xa pro programátory, resp. analytiky, obdobně:
xp = celkové náklady / celkové výkony = (12 mil. Kč + 5 000 xa ) / 0 tis. hodin [*]
xa = celkové náklady / celkové výkony = (18 mil. Kč + 500 xp ) / 15 tis. hodin [**]
Což lze řešit jako soustavu rovnic, vzpomenete-li si na školní léta tak, že z druhé rovnice uděláme vzorec pro jednu z neznámých a ten dosadíme do rovnice první:
xp = [12 000 000 + 5 000 * (18 000 000 + 500 xp) / 15 000] / 10 000
xp = 12 000 000 / 10 000 + 5 000 * (18 000 000 + 500 xp) / 15 000 / 10 000
V doplněné první rovnici pak osamostatňujeme neznámou na jedné straně takto:
(1 - 5 000 * 500 / 15 000 / 10 000) xp = = 1200 + 5 000 * 18 000 000 / 15 000 / 10 000
(1 - 0,25 / 15 ) xp = 1200 + 5 * 1800 / 15
0,9833333334 xp = 1200 + 600
xp = 1800 / 0,9833333334 = 1830,50848
a dosazením do vzorce - druhé rovnice:
xa = (18 000 000 + 500 * 1830,50848 ) / 15 000 = = 1261,01695.
Tyto - věcně správné - výsledky jsou zřejmě úplně odlišné od obou dvojic sazeb spočítaných výše. Připadá-li vám ovšem předcházející postup řešení soustavy rovnic jako složitý, máte pravdu. Teď však použijeme MS Excel. Sestavte nejprve tabulku.
Pro výpočet tabulku upravte následujícím způsobem:
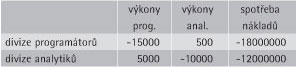
Tuhle úpravu si můžete prostě zapamatovat v následujících dvou krocích:
1. celkové množství výkonů každého procesu za období se odečte od množství případně spotřebovaných výkonů tohoto procesu na příslušném řádku (v tomto případě 0-15000= -15000, resp. 0-10000= -10000)
sloupec spotřebovaných nákladů uvedete se záporným znaménkem.
Tomu, kdo touží chápat smysl této úpravy: stačí si uvědomit, že tabulka nyní představuje "upravenou soustavu" rovnic, které jsme výše označili jako [*] a [**]:
-15 000 xp + 500 xa - 18 000 000 = 0
5 000 xp - 10 000 xa - 12 000 000 = 0
(původní rovnice byly vynásobeny dělitelem pravé strany a všechny nenulové členy byly v obou rovnicích převedeny nalevo).
V tomto tvaru umožňuje MS Excel jednoduchý výpočet řešení soustavy rovnic prostřednictvím funkce "INVERZE", resp. "SOUČIN.MATIC".
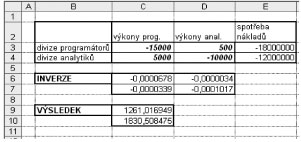
Obě tyto funkce pracují s poli, v jejich argumentu tedy není odkaz na jednu buňku, ale na celé pole buněk, v případě součinu matic dokonce na dvě pole oddělená středníkem:
Např. v buňce C6 je vzorec =INVERZE(C3:D4),
v buňce C9 je vzorec =SOUČIN.MATIC(C6:D7;E3:E4),
což vyjadřuje, že funkce inverze, tj. tzv. inverzní matice se počítá z čísel v podtabulce vyznačené kurzívou (počet řádků a sloupců musí být stejný, jinak funkce indikuje chybu) a funkce součin matic se počítá ze dvou podtabulek s tmavším pozadím (první podtabulka musí mít tolik sloupců, kolik má druhá podtabulka řádků, jinak funkce indikuje chybu).
Dále je třeba vzít v potaz, že jde o tzv. maticové vzorce, které se v Excelu zadávají speciálním postupem vždy najednou pro celou oblast, ve které požadujeme výsledek, ve třech krocích:
1. Označte celou oblast, kam mají být vzorce umístěny (v prvním případě je to C6:D7), kliknutím levým tlačítkem myši (tlačítko stiskněte, ale neuvolňujte) na levý horní roh oblasti (C6)a roztažením při stisknutém levém tlačítku myši na ostatní buňky oblasti. Celá oblast musí zůstat zvýrazněná. Potom levé tlačítko myši uvolněte.
2. Aniž byste dělali cokoli jiného, napište příslušný vzorec s počátečním "=", a netiskněte na závěr klávesu Enter. Vzorec se zobrazí v příslušném podokně MS Excel, celá oblast musí zůstat nadále zvýrazněná. S trochou zručnosti se vám to po několika pokusech podaří i s využitím myši pro vyznačení zadávané podtabulky (což není nutné, jste-li zvyklí zapisovat ručně přes klávesnici adresy okrajových buněk).
3. Aniž byste dělali cokoli jiného, stiskněte současně klávesy CTRL + Shift + Enter. Při dodržení postupu zjistíte, že tentýž vzorec se zapsal do všech buněk označené oblasti uzavřený navíc do složených závorek {}, v jednotlivých buňkách jsou nyní čísla - výsledky maticového výpočtu. Oblast by měla zůstat až do této chvíle označená, následně už můžete provádět cokoli dalšího.
Zkuste si nyní vytvořit přesně stejnou aplikaci, jako je na předcházejícím obrázku tak, že postupně použijete výše uvedený postup pro oba vzorce, v prvním případě zadané maticově do oblasti C6:D7, v druhém případě C9:C10. Dospějete-li ke stejným hodnotám (xp, xa) máte za sebou první nákladovou matici. Výhodou je, že stejnými kroky můžete provést i mnohem složitější výpočet pro mnoho procesů a mnoho neznámých. Kromě delších tahů při označování oblastí to nebude o nic složitější. Musím ovšem upozornit, že některé verze MS Excel jsou omezeny maximálním rozměrem oblasti matice 52 x 52.
K čemu je to dobré?Co vlastně získáme sestavením a výpočtem nákladové matice? Pokud si představíte svůj podnik jako soustavu procesů (výroba, údržba strojů, správa, obchodní podpora, technická podpora, personál, doprava, management), pak některé z nich vytváří finální produkty pro zákazníka a ostatní pak mnoho dalších jiných produktů spotřebovávaných opět v podnikových procesech jako takzvané sekundární zdroje (primárními zdroji nazýváme naproti tomu položky nákladů přímo účtované na každý jednotlivý proces, zejména materiál nebo služby, někdy také mzdy - pokud se nerozhodnete udělat z mezd část nákladu sekundárního zdroje "zaměstnanec" personálního procesu, což je rovnocenná alternativa). Sestavíte-li výchozí tabulku tak, jak je uvedeno na následujícím obrázku, je její zvýrazněná část východiskem pro maticový výpočet přesně stejným postupem, který jsme již absolvovali, s jediným rozdílem, že čtvercová podtabulka "každý s každým" nemá řádky a sloupce jen dva, ale větší počet (stejný pro řádky i sloupce, neboť vždy jde o "turnajovou" tabulku "každý s každým").
Výsledkem maticového výpočtu jsou potom (v jediném sloupci pod sebou obdobně jako nahoře, jen sloupec bude tak dlouhý, jaký rozměr tabulky "každý s každým zvolíme") jednotkové ceny výstupů podnikových procesů - jednotkami nemusí být jen hodiny, ale třeba počty zaměstnanců, strojů, metry čtvereční plochy, kilometry atd.) nákladové ceny produktů interních procesů, samozřejmě již v peněžních jednotkách. Dosadíme-li ceny spotřebovaných produktů podle skutečného množství k zákaznickým produktům a přičteme-li také spotřebu primárních nákladů (příslušná množství jsou jak pro produkty, tak pro náklady v horní, zatím nevyužité části tabulky), máme i přesné "procesní kalkulace" nákladů na produkty. Více ostatně pochopíte, prostudujete-li si následující příklad.
Modelový příklad 1Výrobce přístrojových desek do automobilů (s roční produkcí 5 mil. ks pro tři zákazníky), popsal spotřebu zdrojů ve svých procesech v souladu s navrženým způsobem (viz tabulka na další straně). Úprava pro výpočet matice - použita pole tabulky s tmavším pozadím - a další postup výše popsaným způsobem vypadá následovně (na zvýrazněných tmavších polích došlo k úpravám hodnot dle dříve uvedeného postupu):
Výsledkem jsou tedy nákladové ceny pro jednotku produktu každého z identifikovaných procesů. Např. třetí řádek znamená, že hodina údržby stojí ca. 565 Kč, čtvrtý řádek pak kalkuluje roční náklad na m2 výrobní plochy jako 1280 Kč. Jde o celkové náklady z vyplněných hodnot (součet přímých nákladů v tis. Kč a nákladů spotřeby sekundárních zdrojů, vypočtených jako množství x cena v tis. Kč získaná výpočtem matice).
Pomocí těchto cen pak můžeme stanovit úplné náklady na každý kus výrobku v třech příslušných kategoriích takto - využita je nyní horní část původní tabulky zadání (všimněte si, že jde o úplnou ABC alokaci zadaných ročních nákladů ve výši 36 000 = 10 374,90 + 19 827,90 + 5 797,20 tis. Kč, tato čísla jsme převzali z prvního sloupce tabulky na sudých řádcích):
ShrnutíV předcházejícím textu jsme použili nákladovou matici pro řešení problému stanovení skutečné spotřeby nákladů podnikovými procesy, u kterých se předpokládá vzájemné zacyklení, tj. skutečnost, že procesy spotřebovávají vedle primárních zdrojů - nákladů podniku ve známé výši za časové období také sekundární zdroje, jimiž jsou výstupy jiných procesů nebo dokonce výstupy vlastní, a to pro každý proces samostatně ve známém množství za časové období. Jde například o hledání odpovědi na tyto typové otázky:
> Jak mnoho celkem (peněz) ušetřím na nákladech, když propustím jednoho zaměstnance (výstup podnikového procesu), ujedu měsíčně o tisíc kilometrů méně, sloučím dvě pracoviště do jediného?
> Jak mnoho (peněz) mohu zaplatit dodavateli úklidových služeb, který kompletně zabezpečí realizaci úklidu (výstup podnikového procesu) až doposud zajišťovaného vlastními silami?
> Kolik má zaplatit zákazník, který odbírá jednu třetinu mé celkové kapacity pro výkon servisní činnosti (výstup podnikového procesu)?
> a podobně.
Jak naznačuje poslední otázka, a také celý výše ukázaný modelový příklad, tento postup dává řešení pro podnikovou kalkulaci, dokonce kalkulaci úplných vlastních nákladů produktu, jako speciálního případu výstupu jednoho specifického podnikového procesu (v tomto speciálním případě hlavního procesu, tj. procesu uspokojení zákaznického požadavku). Vedle toho však kalkuluje nákladovou cenu také libovolné vnitřní činnosti v podniku, pokud má měřitelný výstup (a jde tedy o výstup podnikového procesu). Charakteristické vlastnosti tohoto postupu jsou následující:
> Podstatnou roli pro užitečnost výsledku a tím i celého postupu hraje míra vnitřního zacyklení, která může (jako ve výše uvedeném příkladu se dvěma divizemi softwarové společnosti, prodávajících své specifické výkony) - ale v určitých konkrétních případech také nemusí - být významná (například kdyby stejná instituce byla organizována projektově, takže spotřebované výkony jedné nebo druhé divize se promítaly ve skutečně vynaložené výši v jednotlivých projektech přímo zákazníkům - vnitřní zacyklení by v takovém případě bylo odstraněno).
> Neopomenutelným případem vnitřního zacyklení je "procesní kanibalismus", který ve skutečnosti není vůbec řídkým jevem: mzdové účetní si musí spočítat i vlastní výplatu, správce sítě spravuje i svůj počítač a podobně....
> Dostávám vždy kompletní řešení, tedy cenu každého výstupu každého procesu. Základní strukturou je turnajová tabulka "každý s každým" a ve shodě s předchozí poznámkou má na rozdíl od sportovního turnaje plnohodnotný význam i její diagonála. Výsledkem je opět tabulka - matice, obsahující jednotlivě ocenění každého zúčastněného procesu, takže místo výpočtu konkrétní hodnoty jde spíše o sestrojení kompletního (nákladového) modelu. Chceme-li být úplně přesní, můžeme hovořit o modelu nákladových toků podniku, s ohledem na skutečnost, že v průsečíku konkrétního řádku a sloupce výsledkové tabulky najdeme v penězích oceněnou celkovou spotřebu výstupů jednoho procesu (sloupec) procesem druhým (řádek) za určité časové období. O využitelnosti modelu nákladových toků blíže hovoří jedna z následujících samostatných kapitol tohoto článku.
> Jde o rozvrhovou kalkulaci, která dává odpověď na otázku, jak mnoho z celkových nákladů připadá na jeden z pevného celkového počtu procesních výstupů. Neřeší tedy úlohu okamžité úspory peněz v situacích, kdy za již stanoveného počtu vytvořených produktů podnikových procesů jeden určitý produkt přibývá nebo ubývá. V praxi je tedy tato metoda dobře použitelná, rozhodujeme-li o nutné velikosti podniku ještě před jeho založením nebo alespoň v době sestavování rozpočtu na příští rok, zatímco v situaci "ze dne na den", obdobně jako jiné kalkulační rozvrhovací techniky (například přirážková kalkulace nebo neúplná kalkulace s krycím příspěvkem) selhává.
Nákladové ceny na jednotku produktu
Tomáš Nekvapil
Autor je ředitelem divize poradenství společnosti POINT Consulting
V druhé části tohoto článku bude pojednán vztah nákladové metody a metody ABC (Activity Based Costing).
